He seguido la epidemia de coronavirus desde que empezamos a tener noticia de esto como un brote aislado en China. Hacia finales de enero me empecé a inquietar por errores e incoherencias que iban surgiendo sobre todo en China y la OMS - Organización Mundial de la Salud -. De este asunto me ocuparé en un siguiente artículo, y por el momento me basta señalar la siguiente incoherencia.
Hacia finales de enero la expansión de la epidemia en China estaba adquiriendo matices muy preocupantes. Era evidente que las autoridades de China habían perdido el control de la situación, al grado de que millones de personas posiblemente infectadas se les habían fugado del epicentro del problema: la ciudad de Wuhan. Pero pese a eso, la OMS declaró el 23 de enero que el brote de coronavirus en China no era una emergencia internacional de salud pública - ver nota de pie 1 -. Es evidente que la OMS estaba haciendo política más que ciencia al declarar esto. Si no sabían cuántas personas se había fugado de esa ciudad y menos sabían de su destino final…usted concluya.
Ante las incoherencias y errores empecé a considerar a la pandemia como un evento de alta probabilidad. A partir de ese momento me ocupé en diseñar un modelo matemático sencillo para estimar algunas variables críticas de la epidemia, para lo cual acudí a la función matemática de crecimiento exponencial. Algo que también me movió en esto fue mi deseo de advertir a mis amigos y conocidos en mi página de Facebook sobre la naturaleza del problema y los errores que podemos cometer al arranque de la epidemia por nuestra limitada intelección del proceso; errores que a la postre refuerzan el problema. Sin embargo, he decidido avanzar más en la publicación de esto porque algunas cosas que yo anticipaba desde enero se han ido cumpliendo. Pero lo más importante es que, para el caso de México, creo que están ocurriendo cosas muy alentadoras. Y de eso se trata esta primera entrega en esta saga de artículos que espero publicar sobre el coronavirus.
El modelo matemático para el coronavirus
El crecimiento exponencial ocurre cuando la tasa de cambio de una cantidad inicial determinada con respecto al tiempo es proporcional a esa cantidad inicial. Este tipo de crecimiento no es excepcional o raro. Muchas cosas en la naturaleza y el mundo humano tienen este tipo de comportamiento, especialmente en lo que toca a la población de algunas formas de vida, como las bacterias y los virus.
Decidí usar la fórmula del crecimiento exponencial para mis estimaciones. Esta función es la siguiente:
1. xt= x0*bt
donde
xt: el número de contagiados en cualquier tiempo (t)
x0: el número de contagiados al inicio.
b: factor de crecimiento, tasa de contagio o el número de personas contagiadas por cada persona contagiada.
Decidí esto porque hay acuerdo en que las poblaciones de virus crecen de manera exponencial al menos durante la primera fase de una epidemia, mientras la cantidad de sus nutrientes - en este caso personas - no se hayan agotado y permita dicho crecimiento, y no habiendo inmunización artificial disponible. Y éste es precisamente el caso del coronavirus en el momento en que decidí investigar: el inicio de la epidemia en cada país, incluyendo ahora a México.
Reconozco que hay modelos más sofisticados y granulares para predecir eventos en este tipo de situaciones. Pero advierto que la sofisticación de un modelo no otorga garantía de eficacia. Eso ha quedado más que probado durante esta epidemia porque ya tenemos modelos que andaban con muchas ínfulas fallando por montones.
Realicé una sencilla simulación de epidemia con la fórmula 1) con propósitos ilustrativos. Estoy suponiendo que partimos de 1 contagiado, que la tasa de contagio de este virus hipotético es 2 y que no encuentra obstáculos en su propagación. De ese modo, la fórmula 1) ha quedado de la siguiente forma:
2. xt=1*2t
Enseguida le obsequio la gráfica de los resultados de esta simulación.
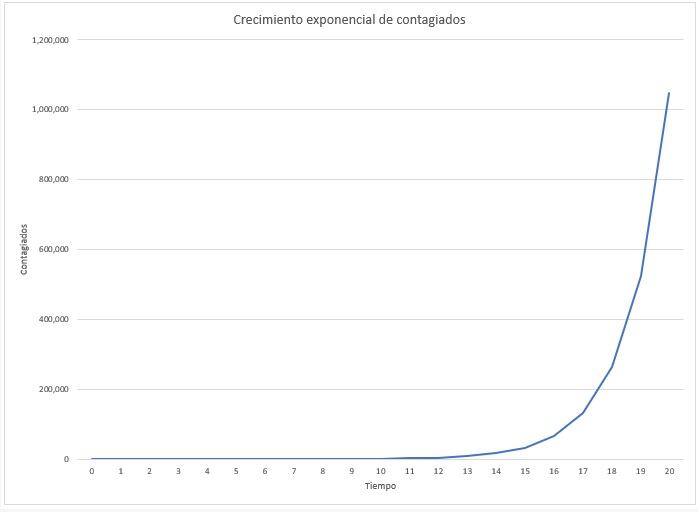
La forma de “J” de la curva es muy parecida a las gráficas que hemos estado viendo por esos tiempos sobre contagiados por coronavirus. En efecto, se trata de un crecimiento exponencial. Y para que se dé una idea del carácter explosivo de este proceso, en esta simulación de epidemia pasamos de una persona contagiada al inicio – tiempo 0 - a poco más de 1 millón de contagiados. Y todo, en tan sólo 20 días.
Lo importante es que esto corrobora que la función de crecimiento exponencial nos puede ayudar a describir la realidad de la epidemia de coronavirus de manera aproximada y al menos en su primera fase.
Pero no cantemos victoria todavía. Cierto que las curvas pueden ser muy parecidas en su forma general, pero eso no significa que la fórmula 1) nos vaya a dar estimaciones correctas sobre la realidad. De hecho, yo usé esta fórmula para mi simulación solo con propósitos ilustrativos, sin pretender jamás que la misma vaya a reflejar la realidad. El hecho es que dicha fórmula no es realista ni de utilidad así, como está, en raw. Usarla así nos llevará a cometer errores muy graves en las estimaciones. Me explico enseguida.
Un error frecuente que cometen los novatos en los números es el usar esta fórmula 1) en raw, como está, para hacer sus proyecciones de epidemia - o cualquier otro evento que presente crecimiento exponencial -. Pero este procedimiento presenta muchos problemas, sobre todo los dos siguientes.
1. Usan tasas de contagio publicadas que no corresponden a su caso de estudio en tiempo y lugar.
Con esto me refiero, por ejemplo, a la habitual práctica de usar la tasa de contagio global, la de China, Italia o cualquier otro país para sus estimaciones en el caso de México. Otro ejemplo de este error es usar una tasa de contagio de hace tres semanas para una estimación desde el hoy. Otro ejemplo es usar una tasa de contagio de un virus parecido al coronavirus. Y este error se refuerza por lo siguiente: a saber, nadie está calculando tasas de contagio en el tiempo para casos específicos, que es lo que pretendo hacer yo en parte.
Al carecer de base estadística, no pueden ofrecer niveles de confianza para sus estimaciones.
Son estos errores, entre otros, los que llevan a cometer graves errores de estimaciones cuando se usa la fórmula 1) como está, en raw.
Así que si queremos que nuestro modelo sea lo más realista posible y útil necesitamos mejorar la fórmula 1) aplicándole algunas transformaciones y métodos matemáticos. Y eso fue precisamente lo que hice para el caso de México y otros países.
Voy a omitir la descripción de las transformaciones y métodos que apliqué a la fórmula 1) porque creo que no son de interés para el lector común. Lo que me interesa poner de relieve son las mejoras que estoy logrando con ese procesamiento matemático adicional de la fórmula. El resultado es un modelo que tiene las siguientes características, entre otras:
2. Permite estimar la tasa de contagio de la epidemia en México. Lo cierto es que el modelo final nos permite estimar la tasa de contagio aun a nivel de estado, municipio, ciudad, localidad, colonia o cualquier nivel de desagregación geográfica, y siempre y cuando se cuente con la información estadística necesaria. Esto es muy importante por lo siguiente.
Al estimar las tasas de contagio en el tiempo para nuestro caso de estudio en tiempo y lugar – en este caso México - le estamos dando más exactitud a nuestras estimaciones. Con esto estamos evitando el error que ya mencioné antes: Usar tasas de contagio publicadas que no corresponden a nuestro caso de estudio en tiempo y lugar. Esto es muy importante porque el coronavirus es diferente a los demás virus y se está comportando de manera diferente por países, regiones y aun según latitudes en el planeta.
La variable más importante a observar durante una epidemia es, no los contagiados, no los muertos ni los recuperados, sino la tasa de contagio. Esto es así porque esta variable es la que nos da la medida de la fuerza de penetración o expansión de la epidemia en la población: si la tasa aumenta con el tiempo, entonces la epidemia está ganando fuerza de penetración; pero si la tasa disminuye con el tiempo, la epidemia está perdiendo fuerza. A su vez, el comportamiento de la tasa de contagio en el tiempo nos permitirá proyectar con algún nivel de confianza el tiempo a futuro en que la epidemia podría terminar.
Y finalmente, estamos resolviendo un problema importante que ya mencioné antes: a saber, nadie está calculando o al menos publicando las tasas de contagio para México, y menos para estados y municipios.
Es un modelo con base estadística. Con esto quiero decir que al menos conocemos el nivel de confianza de nuestras estimaciones, que en nuestro caso estará en el 95%.
Es un modelo dinámico. A medida que el modelo se alimenta con más información de las estadísticas oficiales, mejora su ajuste general y el de sus coeficientes, lo cual mejora su exactitud con el tiempo.
El modelo me ha probado buen ajuste y significancia. Su F crítica y las probabilidades de los coeficientes son menores que 0.05%. Los coeficientes de determinación andan en el rango de 0.91 y 0.98, lo cual significa que el modelo se ajusta bien a la variable que estamos intentando explicar: cantidad de contagiados.
Bien, pues ahora es tiempo de pasar a algunos de los resultados más importantes de este modelo.
La tasa de contagio y algunas proyecciones para México
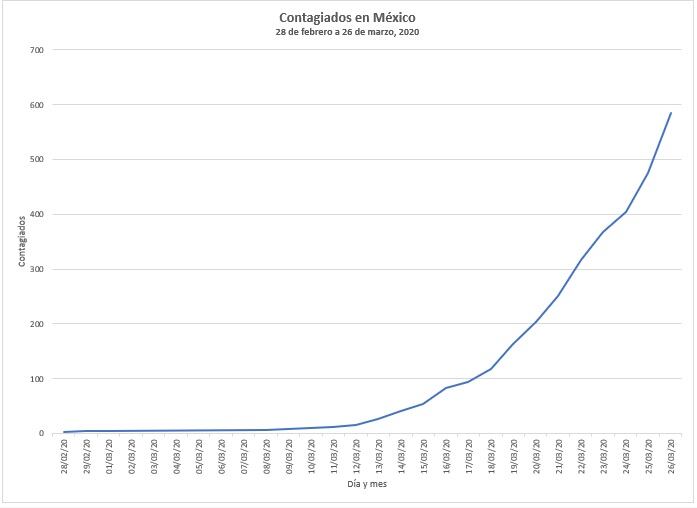
La siguiente gráfica no requiere gran descripción. Representa a los contagiados por coronavirus en México entre el 28 de febrero y el 26 de marzo. El lector puede observar que la forma de la curva se acerca a la “J”, que es la típica del crecimiento exponencial. Pero enseguida se ponen las cosas más interesantes.
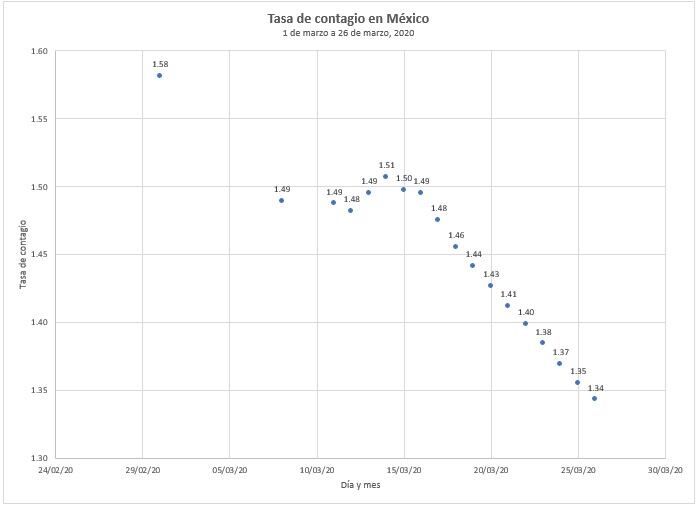
He estado estimando las tasas de contagio para México en el periodo que va del 1 de marzo al 26 de marzo y haciendo proyecciones de contagiados a futuro con un intervalo de confianza del 95% y a partir de las estadísticas oficiales de contagiados. La siguiente gráfica representa las tasas de contagio para México en ese período.
Como puede ver el lector, la tasa de contagio en México está disminuyendo con el tiempo. Tuvo un ligero repunte entre el 12 y el 14 de marzo, cuando pasó de 1.48 a 1.51. Pero en lo esencial, la tendencia de la tasa de contagio es a disminuir con el tiempo, donde ha pasado de 1.58 el 1 de marzo a 1.34 antier, el 26 de marzo.
Si mis estimaciones son correctas, lo anterior significa que el coronavirus ha estado perdiendo fuerza de penetración o de expansión en México a medida que pasa el tiempo. Y para que el lector se dé una idea aproximada de lo que esto significa en términos de disminución de contagiados potenciales le obsequio la siguiente gráfica.
En esta gráfica se representan tres proyecciones de contagiados para México en el periodo que va del 26 de marzo al 5 de abril. Cada curva en la gráfica está usando una tasa de contagio diferente. La curva azul, que es la más alta, está usando la tasa de contagio que dio el modelo el 1 de marzo pasado: 1.58. La curva color naranja usa la tasa de contagio que el modelo estimó para el 15 de marzo: 1.50. Y la curva color gris, la más baja y muy cercana al eje horizontal, está usando la tasa de contagio que el modelo arrojó antier, 26 de marzo: 1.34.
El lector puede apreciar fácilmente el impacto muy significativo que tiene la disminución de la tasa de contagio sobre la proyección de contagiados a futuro: al disminuir la tasa de contagio, disminuye la cantidad de contagiados potenciales. Y en este caso se trata de una disminución muy significativa. Si la tasa de contagio de 1.58 que estaba vigente el 1 de marzo nos llevaba a proyectar poco más de 1.2 millones de contagiados para el 5 de abril, ahora la tasa de contagio de 1.34, vigente hasta antier, permite proyectar tan sólo 18,543 contagiados para el 5 de abril.
Antes de seguir es conveniente hacer dos aclaraciones. En primer lugar, estas estimaciones tienen un intervalo de confianza del 95%. Eso significa que las cifras que le doy están en un intervalo con un mínimo y un máximo, y lo que estoy consignando son las estimaciones centrales dentro de ese intervalo. En realidad, las cifras podrían estar por arriba o por abajo de esa medida central y dentro de ese intervalo, con un 95% de confianza.
En segundo lugar - y lo más importante -, los resultados del modelo en cuanto a tasas de contagio no entran en contradicción con la realidad de contagiados en crecimiento. Esto es así porque la tasa de contagio puede disminuir aun y cuando la cantidad nominal de contagiados esté aumentando. A la larga, y si esto se sostiene, la misma disminución de la tasa llevará a una disminución en el registro de contagiados.
Creo que a estas alturas ya habrá quedado claro el gran contenido de verdad de algo que dije arriba. Lo repito:
“La variable más importante a observar durante una epidemia es, no los contagiados, no los muertos ni los recuperados, sino la tasa de contagio. Esto es así porque esta variable es la que nos da la medida de la fuerza de penetración o expansión de la epidemia en la población: si la tasa aumenta con el tiempo, entonces la epidemia está ganando fuerza de penetración; pero si la tasa disminuye con el tiempo, la epidemia está perdiendo fuerza. A su vez, el comportamiento de la tasa de contagio en el tiempo nos permitirá proyectar con algún nivel de confianza el tiempo a futuro en que la epidemia podría terminar.”
Desde luego que la información que hemos visto hasta aquí son excelentes noticias para México, siempre y cuando mis estimaciones sean correctas. Lo que nos resta ahora es indagar las posibles causas de la disminución de la tasa de contagio en México. Sobre esto sólo podemos especular porque no tenemos información suficiente. Por el momento, se me ocurren las siguientes causas posibles:
1.El clima en México.
2.El trabajo del gobierno.
3. El estrato de la población según edad.
4. El estrato socioeconómico
5. “Errores” en las estadísticas oficiales.
El clima en México
Como el coronavirus es un agente nuevo, lo que conocemos de él se ha ido recopilando al paso gracias a investigaciones científicas. Aunque el apresuramiento de estas investigaciones las hace muy vulnerables al error, como ha sucedido con frecuencia, parece que hay acuerdo en algunas cosas importantes. Un punto en el que hay acuerdo hasta el momento es que el coronavirus, al igual que el virus de la gripa normal, es muy sensible a los rayos UV, al calor y la humedad.
En marzo 10 fue lanzado un estudio que concluye que la alta temperatura y la alta humedad reducen de manera significativa la capacidad del virus para propagarse de persona a persona, lo que es la tasa de contagio. Y este resultado, dicen en dicho estudio, es consistente con lo que le sucede al virus de la gripa normal con la temperatura y la humedad - ver nota de pie 2 -.
Casi al mismo tiempo la Universidad de Maryland y la Red Mundial de Virus – GVN – publicaron un estudio que afirma que el coronavirus sigue un patrón estacional similar a otros virus respiratorios como la gripe estacional. Para precisar, el estudio encontró que los países y ciudades que experimentan la epidemia de manera significativa tienen climas invernales similares con una temperatura promedio que va de 5° a 11° C y una humedad promedio de 47 a 79 %. Todos estos sitios se ubican en una franja este-oeste a lo largo de la misma latitud 30-50 N. Algunos de los sitios que están en esta franja son: Wuhan, Corea del Sur, Japón, Irán, el norte de Italia, Seattle y el norte de California, que ya sabemos son puntos críticos del problema - ver nota de pie 3 -.
Pues bueno, lo que sabemos es que México no está en esa franja y ya está registrando al menos altas temperaturas. Es por esto que yo creo que el clima en México puede ser la causa más importante en la disminución de la tasa de contagio.
El trabajo del gobierno
Pese a que el gobierno no ha implementado una política de choque, como en el caso de China, y pese a que ha sido un tanto relajado en las políticas de restricción a la movilidad humana, no se descarta que el cierre de algunas actividades y la práctica del distanciamiento social promovidas por el gobierno estén colaborando en la disminución de la tasa de contagio.
El estrato de la población según edad
Ya se sabe que el coronavirus está atacando con mayor fuerza destructiva a las personas de avanzada edad y con problemas de salud sistemáticos, y que parecen ser el 20% de los contagiados. Se puede creer que este factor sea muy importante en el caso de Europa y sobre todo de Italia, porque se trata de poblaciones viejas. Pero ocurre que México es una población mayormente joven. Esto podría ser otro factor en la disminución de la tasa de contagio en México. No porque los jóvenes y niños sean inmunes, sino por los problemas técnicos que tiene el registro administrativo de contagiados, lo cual veremos más abajo.
El estrato socioeconómico
Como el virus es importado en el caso de México, siempre será de máxima probabilidad que los primeros portadores sean personas ubicadas en los estratos socioeconómicos altos. Esto podría ayudar a disminuir la tasa de contagio porque cabría esperar que la capacidad de contención del virus sea mayor en los estratos altos que en los bajos. Después de todo, una persona con altos ingresos siempre puede atenderse mejor y estar en cuarentena por largo tiempo sin ver mermado su nivel de vida. El caso de China es ejemplo de lo que ocurre con un brote que detona en el estrato bajo. El coronavirus detona en una zona de estrato bajo de Wuhan, y desde ahí se propaga de manera explosiva.
Así que este factor también puede ser una causa en la disminución de la tasa de contagio en México.
“Errores” en las estadísticas oficiales
A primera vista no deja de ser muy extraño que la tasa de contagio en México esté disminuyendo casi sistemáticamente desde el 1 de marzo. Extraño, porque estamos en la fase inicial de la epidemia, que es cuando el virus crece de manera exponencial, lo cual debería reportar una tasa de contagio más o menos constante o creciente. Sólo eso nos daría motivos para especular en torno a la posibilidad de que el gobierno esté subestimando a los contagiados deliberadamente o no.
En lo personal, yo no estoy dispuesto a creer que el gobierno esté subestimando la cantidad de contagiados con el propósito de engañarnos. Mi imaginación no da como para insertar semejante disposición al crimen en la voluntad de AMLO. Además, no es un hombre tonto. Él debe saber que ocultar la información es un balazo en los pies mañana. Lo que sí resulta al menos verosímil es que la subestimación se deba a las limitaciones técnicas en los sistemas administrativos. Y hay varios datos ya corroborados que podrían apoyar esto último.
A estas alturas se sabe que alrededor del 80% de los contagiados son asintomáticos o leves. En su gran mayoría, estos casos no son reportados ni registrados. De hecho, en algunas de mis estimaciones desde enero yo he estado trabajando bajo el supuesto de que el 75% de los contagiados no están registrados – no es el caso de estas proyecciones para México -. También se sabe que las pruebas para el coronavirus no son infalibles. Sólo el día de ayer reportaban que las pruebas en España - importadas desde China, por cierto - tenían una muy baja eficacia: 30%. Estaban determinando como negativos a muchos casos positivos.
En suma, tal vez los contagiados reales son mucho más que los registrados y sospechosos, y tanto como el 80% del total, pero los gobiernos tienen serias limitaciones técnicas para conocer su monto. Y ya hay algunas investigaciones que soportan esta conclusión.
Si esto está ocurriendo en México, entonces esto podría estar atenuando artificialmente la tasa de contagio. Sin embargo, me parecería injusto culpar a AMLO por una limitación técnica que por el momento excede toda posibilidad humana.
Ahora bien, suponer que la tasa de contagio debe ser constante o creciente en México solo porque estamos en la fase inicial de la epidemia, es mera teoría. Esto no se trata de una demostración silogística, de tal modo que las cosas no tienen que suceder así necesariamente, y menos cuando el análisis estadístico prueba que la tasa de contagio está disminuyendo en México.
Así que la verdad de fondo puede ser la que ya enuncié anteriormente: que la epidemia está perdiendo fuerza en México casi de manera sistemática, y que esto puede deberse a algunas o todas las causas que ya abordé. Y esto se sostiene al menos para los casos en registro, que ya pueden ser una muestra aleatoria muy respetable. Después de todo, esta explicación va en consonancia con los resultados del modelo que hemos usado.
Pero es tiempo de concluir esta primera parte de la saga de artículos que espero publicar sobre el coronavirus. Por cierto que los siguientes capítulos serán más breves. Éste se nos fue de largo por las gráficas y explicaciones en torno al modelo matemático.
Y recuerde: no colabore con el virus. Ponga segura distancia de los demás, lávese las manos, cuídese y cuide a sus seres queridos. Parece que está funcionando.
Advertencias:
No debe olvidar que un “modelo” es solo un concepto científico. Más precisamente, es un concepto que consiste en la especificación de una teoría científica tal que consienta la descripción, explicación y anticipación de un campo determinado de la realidad. Como tal, es una construcción ideal que no se ha de cumplir necesariamente porque no tiene garantía total en virtud de la limitación y falibilidad de la ciencia. Sin embargo, esto no le resta toda utilidad a los modelos. Pese a sus limitaciones, los modelos nos dan el poder para describir, explicar y anticipar eventos con algún grado tolerable de error probable.
No necesariamente los modelos más sofisticados y granulares son los mejores. El principio de parsimonia de Ockham sigue teniendo vigencia, de tal modo que, en igualdad de condiciones, la explicación más sencilla suele ser la más probable.
Aunque el tipo de modelo que implementé suele ser el mejor para estimar el factor de crecimiento – o tasa de contagio -, tiene un cierto margen de error. Además, solo se ajusta bien a las fases de entrada y salida de una epidemia, cuando la tasa de contagio tiene alguna dinámica en el tiempo.
Notas de pie:
https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3551767
Le comparto enlace a mi blog personal donde encontrará el acervo completo de artículos que he publicado en este diario:
También le doy enlace a mi página de Facebook:
https://www.facebook.com/pages/El-Nolato/478609918855888?fref=ts
